一、聚类定义
聚类分析(cluster analysis)是一组将研究对象分为相对同质的群组(clusters)的统计分析技术。 聚类分析区别于分类分析(classification analysis) ,后者是有监督的学习。
- 依据研究对象(样品或指标)的特征,对其进行分类的方法,减少研究对象的数目。
- 各类事物缺乏可靠的历史资料,无法确定共有多少类别,目的是将性质相近事物归入一类。
- 各指标之间具有一定的相关关系。
变量类型:定类变量、定量(离散和连续)变量
二、划分聚类方法-Kmeans:
对于给定的样本集,按照样本之间的距离大小,将样本集划分为K个簇。让簇内的点尽量紧密的连在一起,而让簇间的距离尽量的大。
- 步骤1:取得k个初始中心点
- 步骤2:利用中心点划分样本集为k个簇
- 步骤3:根据已经被分类的数据分别重新计算各自的中心点,如果中心点发生变化回到步骤2,未发生变化转到步骤4
- 步骤4:收敛
缺点:
初始值敏感、采用迭代方法,得到的结果只是局部最优、K值的选取不好把握、对于不是凸的数据集比较难收敛
如何衡量Kmeans 算法的精确度?
SSE(Sum of Square Error) 误差平方和, SSE越小,精确度越高。
三、改进算法-二分Kmeans
- 首先将所有点作为一个簇,然后将其一分为二。
- 每次选择一个簇一分为二,选取簇的依据取决于其是否能最大程度降低SSE即选取聚类后SSE最小的一个簇进行划分。
- 直至有k个簇
四、Kmeans Code
import numpy as np
import matplotlib.pyplot as plt
import scipy.io as scio
# %matplotlib inline
def K_Means(X, sp, K):
# 计算临近点
def near(p):
dis = [np.sum(np.square(x-p)) for x in sp]
return dis.index(min(dis))
# 打印结果
def print_result(sp_list):
#打印中心点迭代轨迹
sp_list = [np.array([x[k] for x in sp_list]) for k in range(K)]
for k in range(K):
plt.plot(sp_list[k][:,0], sp_list[k][:,1], 'k->', label='type{}'.format(k))
#分类打印其他点
p_list = [[] for k in range(K)]
for p in X:
i = near(p)
p_list[i].append(p)
p_list = [np.array(x) for x in p_list]
color = ['r','g','b']
for i in range(K):
plt.plot(p_list[i][:,0], p_list[i][:,1],color[i]+'o')
plt.title('K-Means Result')
plt.xlabel('X')
plt.ylabel('Y')
plt.legend('123')
plt.show()
# 迭代中心点
sp_list = []
sp_list.append(sp)
while True:
count = np.zeros(K)
sp_t = np.zeros((K,2))
for p in X:
i = near(p)
count[i] += 1
sp_t[i] += p
sp_t = np.array([sp_t[i]/count[i] for i in range(K)])
SSE = np.sum(np.square(sp-sp_t))
if SSE < 0.001:
break
sp = sp_t
sp_list.append(sp)
print_result(sp_list)
print('聚类中心:')
for p in sp:
print(p, end=',')
if __name__ == '__main__':
data = scio.loadmat('ex7data2.mat')
X = data['X']
K = 3
sp = np.array([[3, 3], [6, 2], [8, 5]]) # starting point
K_Means(X, sp, K)
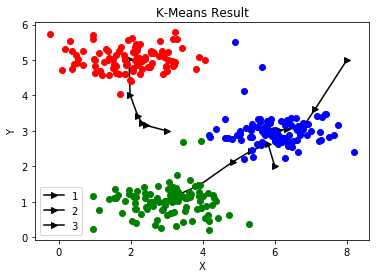
K为3聚类中心: [1.95399466 5.02557006],[3.04367119 1.01541041],[6.03366736 3.00052511]
[测试数据下载地址]: ex7data2.mat
[参考资料]:K-Means聚类算法原理




